Tetris

Memory limit: 32 MB

You have probably had an opportunity to play Tetris. In this game, there are two-dimensional blocks falling vertically onto the platform. A block is falling down, till it reaches a barrier - another block or the platform. Once stopped, the block does not move anymore.

In the original game of Tetris, fully filled lines of blocks disappear, but for the sake of simplicity, we do not consider disappearing in this task. Additionally, let us assume that all blocks are horizontal stripes of height 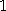. Furthermore, it is not allowed to rotate or move blocks. The only thing which can be changed, is the order in which the blocks are going to fall. Given the sizes and the horizontal offsets of all blocks, find such an order of blocks, that the height of the figure obtained if they are dropped in this order will be as small as possible.

Task

Write a program, which:

• reads the description of blocks,
• finds such an order of blocks, that the height of a figure obtained from them is minimized,
• writes the answer to the standard output.

Input

In the first line of the standard input there is one integer (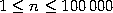), denoting the number of blocks, which are about to fall onto the platform. Each of the following lines contains two integers 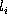and 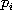(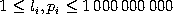), separated with a single space and denoting adequately the length of 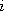-th block and the horizontal offset of the left side of the block.

Output

The first line of the standard output should contain one integer, denoting the smallest possible height of the figure obtained from the given blocks. Following lines should contain the description of the order of the blocks, for which the height of the obtained figure is minimized. In the 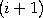-th line of the output there should be one integer, denoting the sequence number of the block, which should fall as the 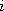-th. The blocks are numbered from 1 to in the same sequence as they appear in the input.

If more than one correct solution exists, your program should output any of them.

Example

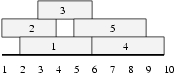
For the input data:

5
4 2
3 1
3 3
4 6
4 5

the correct result is:

3
1
4
5
2
3

Task author: Jakub Radoszewski.